When designing your own bags, calculating the volume it can carry when filled can be a bit of a tricky task. We do not have access to the industry standard method, which is filling it full of small balls of a known size and using this to calculate the volume. Although an industry standard, it does not mean all manufacturers use this method!
For this article we are going to simplify this problem by assuming a 3D rectangle – a cuboid or rectangular prism. More complicated shapes will take further consideration.
The first step most people take is using the fabric panel dimensions, and doing the simple
width * height * depth
calculation. This is great for calculating the volume of a rigid object, but bags are soft and therefore deform. This curvature greatly changes the actual volume a bag can contain.
TL/DR: Its complicated, and don’t stress it too much. It is difficult to compare to commercial products
Pattern Pieces to Finished Bag Volume
Assuming a simple cube or rectangular cuboid shape, using the measurements of your fabric panels multiplied to get the volume is a simple way to estimate. However, bulging and deformation result in a different actual volume.
The idea that a bag has a different volume when filled compared to the fabric dimensions may seem a bit of an odd concept, because the surface area does not change, and the fabric essentially does not stretch.

Take the example on the left on this image, the flat square (e.g a teabag or sandwich bag). Doing the fundamental width * height * depth calculation would result in it having zero volume as it has no depth (just two identical flat pieces of fabric sewn together). However, when it is filled, it clearly bulges out and has volume. For a constant surface area (no material stretching), a sphere is the shape with the maximum volume, so your bag trends towards this. The seams do not allow it to form a true sphere, so you end up with the familiar pillow case shape.
With the tea bag example, the relative volume change from flat to inflated is dramatically large. With a cuboid shape, the relative change is still significant but not as dramatic.
So how can you estimate the volume based on the dimensions of your pattern pieces?
After running many fabric volume inflation simulations in Blender for a variety of common bag shapes (flat pouches, backpacks, bike frame bags), I’ve come to some very generalised rules:

Cuboid (Rectangular) Bag Volume Calculator
Multiply the width * height * depth of the fabric panels to get the geometric volume then multiply by 1.2 to get a more accurate estimation of the volume when bulged out
Volume: 0 Litres
Volume x 1.2: 0 Litres
If interested, this is similar to the the mathematical solution for the maximum volume of a inflated 1x1x1 cube is which is approximately 1.2 (Pak and Schlenker 2009). My estimate of the 1.2 multiplier comes from inflating a variety of non-cube shapes which vary from slightly flat to rectangular, approximating typical backpack dimensions.

Alternative Cuboid (Rectangular) Bag Volume Calculator
You can also assume the bulging causes the bag to form an elliptical cylinder. This estimate gives typically an over-estimate, because back panels and stiffeners tend to help the fabric resist forming a cylinder shape.
Cylinder Volume Calculator
Volume: 0 Litres

Narrow Bag Volume Estimation
Multiply by 1.5 to 2 for a rough estimate.
This may seem like a very large increase. However, my bike frame bag has a narrow depth compared to width+height, and has a volume of 3.8 litre if you just calculate the geometrical volume of a triangular prism. But running a fabric simulation to inflate it results in a filled volume of 6.1 litre (1.6 times larger). The narrower the bag, the larger the factor (approaching the paper bag problem below). The tension from attaching it to the frame will however, reduce this filled volume a little.

Flat Bags (Pouches) Volume Estimation
You can use a paper bag problem solution to calculate the maximum filled volume:
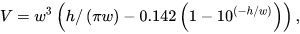
w is width and h is height in metres, and V is volume in m3
Paper Bag Volume Calculator
Result: 0 Litres
If interested, the mathematical solution for the maximum volume of a 1×1 teabag is 0.19 (Pak and Schlenker 2009)
Which Method is Best?
So far for the cuboid shaped bags we have used the width, height and depth of the fabric panels and calculated 3 different volumes for the same bag! Which highlights that it is difficult to compare volumes between manufacturers, because how do you know how they have measured it? For your own projects, use something between the ideal cuboid (width x height x depth) and the cylinder. You could use the average of the two, or the cuboid * 1.2 which is a rough estimate based on fabric simulations.
As a real world example, I have a commercially made backpack quoted at 25L, which is a very convenient rectangular cuboid shape. Measuring the fabric panels width x height x length gives a volume of 19L. Assuming a cylinder by calculating the circumference from the fabric panel widths and depths gives 26L (the same as calculating the elliptical cylinder from the filled bag dimensions as explained below). A 3D software fabric simulation with a low internal pressure gives 24L. Taking an average between the width x height x depth and the cylinder will get your own estimates in the right ballpark.
A final way of calculating the volume: If you are familiar with the 3D modelling software Blender, simulating volume is easy by adding a “Simple” subdivision surface multiplier then cloth physics, which is how I generated the above simulations.
Calculating Volume from a Made and Filled Bag
For the inverse problem, trying to calculate the volume of a made bag (cuboid shaped e.g. a backpack), again it is best to avoid doing a simple width * height * depth calculation of your actual fabric pieces as this does not account for bulging.
Instead, you can use the equation for calculating the volume of a elliptic cylinder using the actual puffed out bag dimensions, not the fabric panels width and height themselves.
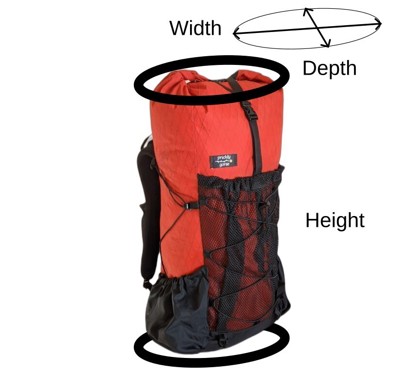
Filled Bag Volume Estimation
Volume: 0 Litres



